7330. Делимость на 3

Рассмотрим последовательность 1, 12, 123, 1234, 12345, 123456, 1234567, 12345678, 123456789, 12345678910, 1234567891011, ....

Подсчитайте, сколько элементов этой последовательности среди первых n делятся на три.

Вход. Одно натуральное число n (1 ≤ n ≤ 2³¹ – 1).

Выход. Выведите одно найденное число.

Пример входа	Пример выхода
4	2

РЕШЕНИЕ

математика

Анализ алгоритма

Пронумеруем элементы последовательности: a₁ = 1, a₂ = 12, a₃ = 123, … . Посмотрим, какие числа последовательности делятся на 3:

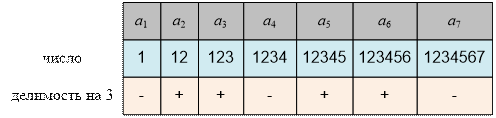
Можно заметить, что на 3 делятся элементы a_i, где i mod 3 ≠ 1.

Если n mod 3 = 0, то количество элементов в последовательности a₁, a₂, …, a_n делится на 3. Среди них имеется в точности n / 3 * 2 таких, что делятся на 3.

При n mod 3 = 1 количество делящихся на 3 элементов будет n / 3 * 2, а при n mod 3 = 2 их будет n / 3 * 2 + 1.

Реализация алгоритма

Читаем значение n.

scanf("%d",&n);

Вычисляем и выводим ответ.

res = n / 3 * 2;

if (n % 3 == 2) res++;

printf("%d\n",res);

Python реализация

Читаем значение n.

n = int(input())

Вычисляем и выводим ответ.

res = (n // 3) * 2

if n % 3 == 2: res += 1

print(res)